


Next: 1 はじめに
Up: 高速多重極展開法とツリー法---多体シミュレーションのための高速算
法
Fast multipole
Previous: 高速多重極展開法とツリー法---多体シミュレーションのための高速算
法
Fast multipole
I overview the Fast Multipole Method (FMM) and the Barnes-Hut tree
method. These algorithms evaluate mutual gravitational interaction
between N particles in 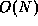 or
or 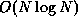 times, respectively.
I present basic algorithms as well as recent developments, such as
Anderson's method of using Poisson's formula, the use of FFT, and
other optimization techniques. I also summarize the current states of
two algorithms. Though FMM with
times, respectively.
I present basic algorithms as well as recent developments, such as
Anderson's method of using Poisson's formula, the use of FFT, and
other optimization techniques. I also summarize the current states of
two algorithms. Though FMM with 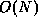 scaling is theoretically
preferred over
scaling is theoretically
preferred over 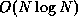 tree method, comparisons of existing
implementations proved otherwize. This result is not surprizing, since
the calcultion cost of FMM scales as
tree method, comparisons of existing
implementations proved otherwize. This result is not surprizing, since
the calcultion cost of FMM scales as 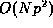 where p is the order
of expansion, while that of the tree method scales as
where p is the order
of expansion, while that of the tree method scales as 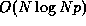 .
.
Jun Makino
Tue Sep 1 21:46:06 JST 1998
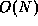 or
or 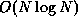 times, respectively.
I present basic algorithms as well as recent developments, such as
Anderson's method of using Poisson's formula, the use of FFT, and
other optimization techniques. I also summarize the current states of
two algorithms. Though FMM with
times, respectively.
I present basic algorithms as well as recent developments, such as
Anderson's method of using Poisson's formula, the use of FFT, and
other optimization techniques. I also summarize the current states of
two algorithms. Though FMM with 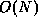 scaling is theoretically
preferred over
scaling is theoretically
preferred over 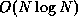 tree method, comparisons of existing
implementations proved otherwize. This result is not surprizing, since
the calcultion cost of FMM scales as
tree method, comparisons of existing
implementations proved otherwize. This result is not surprizing, since
the calcultion cost of FMM scales as 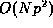 where p is the order
of expansion, while that of the tree method scales as
where p is the order
of expansion, while that of the tree method scales as 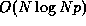 .
.