
Figure 2: A globular cluster, M15, as seen by the Hubble Space Telescope[4]
A globular star cluster [fig. 2; [4]] typically contains about a million stars, packed together much closer than the stars in the solar neighborhood. Such a cluster describes a wide orbit around the parent galaxy, well separated from the stars in that galaxy. If we would live in the core a dense globular cluster, the brightest stars would appear as bright as the full moon, which would make them too bright too look at directly, given their point-like nature. Optical astronomy of anything but the nearby stars in the same globular cluster would be rather difficult, in such a situation.

Figure 2: A globular cluster, M15, as seen by the Hubble Space
Telescope[4]
In the simplest approximation, we can study a globular cluster as a collection of point masses, reducing the problem to the gravitational N-body problem, which was solved by Newton for N=2, but was only studied in detail for N>2 when computers became available. Any localized distribution of particles will tend to become spherical, as a result of forgetting the initial conditions, on a two-body relaxation time scale:

where the crossing time 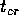 is a measure for the time it takes
for a typical star to move across the cluster.
is a measure for the time it takes
for a typical star to move across the cluster.
Heat is transported through the cluster, as a consequence of many
two-body encounters, on the time scale 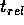 . On longer time
scales, any self-gravitating star system is unstable. Since the
system tends to relax towards a Maxwellian velocity distribution,
there are always some stars that acquire a velocity that exceeds the
escape velocity, after which they are lost from the system. Other
stars tend to congregate in the central regions which grow denser at
an ever-increasing rate, because higher density implies more frequent
encounters and hence a faster two-body relaxation.
. On longer time
scales, any self-gravitating star system is unstable. Since the
system tends to relax towards a Maxwellian velocity distribution,
there are always some stars that acquire a velocity that exceeds the
escape velocity, after which they are lost from the system. Other
stars tend to congregate in the central regions which grow denser at
an ever-increasing rate, because higher density implies more frequent
encounters and hence a faster two-body relaxation.
This run-away redistribution of energy and mass leads to a phenomenon
called gravothermal collapse, often called core collapse, which
takes place on a time scale 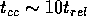 . Core collapse
was hinted at in numerical simulations [5] in the 1960s,
and verified through direct N-body simulations
[6] and modeled by semianalytic methods
[7] in the 1970s.
Core collapse is a fundamental feature of long-term stellar-dynamical
evolution, showing the instability that results from the negative
specific heat inherent in self-gravitating systems. During core
collapse, at first the system can be modeled as passing through a
series of self-gravitating equilibrium models exhibiting a maximum
entropy for a finite central concentration. Once this maximum is
passed, subsequent evolution will increase the entropy, and the
structure of the star cluster is forced to deviate from that of an
equilibrium model.
. Core collapse
was hinted at in numerical simulations [5] in the 1960s,
and verified through direct N-body simulations
[6] and modeled by semianalytic methods
[7] in the 1970s.
Core collapse is a fundamental feature of long-term stellar-dynamical
evolution, showing the instability that results from the negative
specific heat inherent in self-gravitating systems. During core
collapse, at first the system can be modeled as passing through a
series of self-gravitating equilibrium models exhibiting a maximum
entropy for a finite central concentration. Once this maximum is
passed, subsequent evolution will increase the entropy, and the
structure of the star cluster is forced to deviate from that of an
equilibrium model.
Even in an idealized system of self-gravitating point particles, core collapse will be halted before an infinite central density is reached. When the central density is high enough, occasional close encounters between three unrelated particles will form bound pairs (binary stars in the case of star clusters), with the third particle carrying off the excess kinetic energy required to leave the other two particles bound. Subsequent encounters between such pairs and other single particles tend to increase the binding energy of these pairs, which leads to a heating of the surrounding system of single particles.
When enough pairs have been formed in this way, the resulting energy
production will reverse the process of core collapse. After reaching
a minimum radius and a maximum density, the core region will expand
again. Core collapse, when threatened to occur by the collective
effects of two-body relaxation, can thus be narrowly averted by a
handful of crucial three-body or four-body reactions in the dense
core of a nearly collapsed cluster. What will happen next depends on
the total number N of particles in the system. If this number is
sufficiently small, 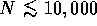 , the whole system will
slowly and steadily expand. In this case a steady-state equilibrium
can be found between the steady energy production in three-body
encounters in the center, and the continuous loss of energy through
the outskirts of the system.
, the whole system will
slowly and steadily expand. In this case a steady-state equilibrium
can be found between the steady energy production in three-body
encounters in the center, and the continuous loss of energy through
the outskirts of the system.
If the total number of particles exceeds 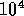 , however, a
different behavior emerges. The more particles there are in the
system, the higher the central density has to become to halt core
collapse. As a result, the post-collapse phase features a short
relaxation time in the center of the cluster, shorter than the
relaxation time in the outer regions, where most of the particles can
be found. From the point of view of the inner core dynamics, the bulk
of the mass further out seems almost frozen. It is this discrepancy
in time scales that can cause the inner core to become `impatient',
and to revert to a local collapse, triggered by the slightest
fluctuation in the direction of the energy flow produced by stochastic
three- and four-body interactions.
, however, a
different behavior emerges. The more particles there are in the
system, the higher the central density has to become to halt core
collapse. As a result, the post-collapse phase features a short
relaxation time in the center of the cluster, shorter than the
relaxation time in the outer regions, where most of the particles can
be found. From the point of view of the inner core dynamics, the bulk
of the mass further out seems almost frozen. It is this discrepancy
in time scales that can cause the inner core to become `impatient',
and to revert to a local collapse, triggered by the slightest
fluctuation in the direction of the energy flow produced by stochastic
three- and four-body interactions.
What happens then is that about 1% of the inner particles will go into a coherent collapse, locally reminiscent of the original core collapse. As before, bound pairs of particles spring into action, generate energy, and manage to reverse the collapse in the nick of time, preventing an infinite central density from building up. This process repeats itself, leading to irregular oscillations of the core of the cluster.
The existence of these oscillations was unknown until 1983, when they were first found in approximate simulations [8]. Dubbed `gravothermal oscillations', they were subsequently analyzed in detail with semi-analytic methods [9]. Their occurrence was confirmed in a variety of approximate numerical simulations [10], and shown to correspond to low-dimensional chaos for large N values [11]. Direct verification of the existence of these oscillations was attempted, using the fastest supercomputers available, but these attempts were unsuccessful [12,13].
The reason that they were so hard to confirm through direct N-body simulations lies in the fact that it has not been possible to model star cluster evolution with more than 10,000 particles until the advent of the GRAPE-4. This may seem surprising, given the fact that cosmological simulations now routinely handle up to a billion particles. The main difference between the two type of calculations lies in the higher accuracy required for star cluster simulations, together with the much larger number of time steps required, in comparison with cosmological simulations.
As for the first point, following the gravothermal collapse requires a very accurate integration of the equations of motion. The required accuracy is difficult to achieve using approximate schemes like tree codes [14]. Therefore, traditional direct summation schemes have to be used. Even on supercomputers the maximum particle number is thus limited to about ten thousand.
The second point is related to the fact that N-body simulations play a very different role in the modeling of star clusters, and of cosmological large-scale structure formation. In the case of star clusters, each particle stands for an individual star, and thus has a direct physical meaning. In the case of a cosmological simulation, each galaxy is represented by a relatively small number of particles, that sample the distribution of stars in phase space. Each particle thus represents the average behavior of many millions of stars. The time steps used can therefore be much larger than would be the case if we were to follow the close encounters of individual stars.
Finally, the existence of gravo-thermal oscillations was proven when they were seen in a direct N-body simulation on the GRAPE-4 that was able to incorporate N values beyond N=10,000 [15], as illustrated in figures 3 and 4.
After core collapse, the fluctuations in central density grow with increasing N values, as is clear from figure 3. For the largest N values displayed, the typical behavior of core oscillations emerges, with its deep and long-lasting throughs punctuated with brief interludes of high core density. For smaller N values, some oscillatory behavior seems to be present, but less pronounced. The results of the central density evolution, while suggestive, do not answer the question of the existence of gravothermal oscillations.
Figure 4, however, provides the proof of the gravothermal nature of these oscillations [16]. The thermodynamic cycle exhibited by the central density and `temperature' (as measured by the velocity dispersion), is traversed in the opposite direction from that of a Carnot engine: the decompression stage takes place at a lower temperature than the compression stage. This is a reflection of the negative heat capacity of self-gravitating systems: compression leads to a temperature increase resulting in more heat loss and hence more compression, with the opposite effects holding during decompression. The period of decompression finishes when the core expands beyond the central isothermal area.
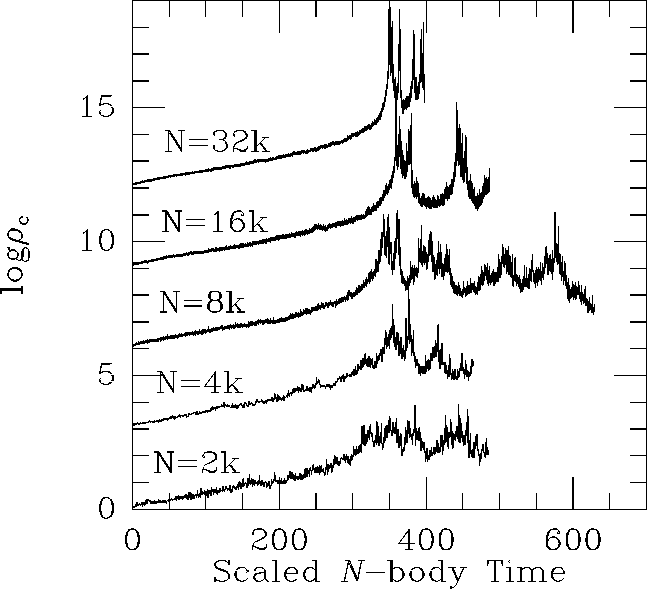
Figure 3: The evolution of the central density 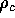 . Thirty time units
correspond roughly to one initial half-mass relaxation time.
Curves for different values of N are vertically
shifted by 3 units.
. Thirty time units
correspond roughly to one initial half-mass relaxation time.
Curves for different values of N are vertically
shifted by 3 units.
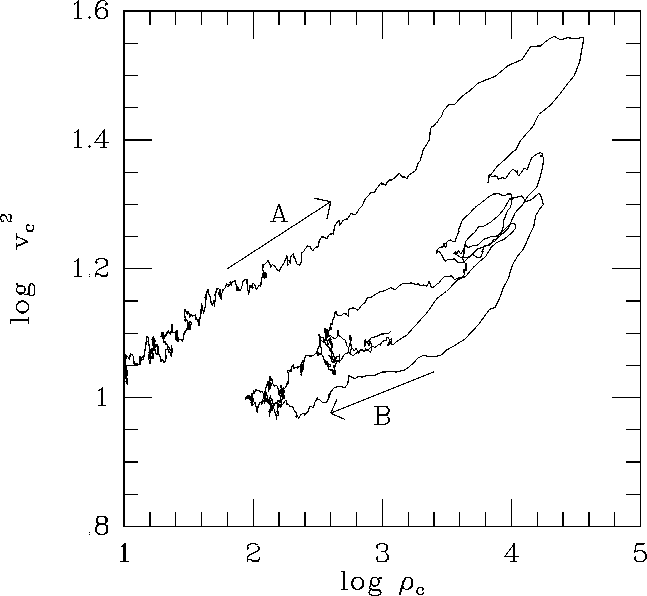
Figure 4: Changes in central density 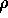 and central velocity
dispersion
and central velocity
dispersion 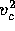 , for a simulation with 32k particles. Each data
point presents a time average, obtained by averaging
, for a simulation with 32k particles. Each data
point presents a time average, obtained by averaging 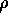 and
and
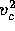 over 80 snapshots. Arrows indicate the direction of
evolution.
over 80 snapshots. Arrows indicate the direction of
evolution.
Having clarified the fundamental behavior of self-gravitating point mass systems, in the limit of very large numbers of particles, we are currently working on more realistic treatments of star clusters, where the evolution of individual stars is modeled [17].