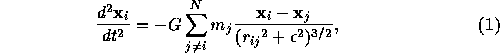
We plan to complete GRAPE-6 with the peak speed of 200 Tflops by year 2000. On the other hand, the peak speed of the fastest general-purpose computer has been increasing by a factor of 100 per decade for the last half century. This trend is expected to continue for at least next 10--20 years. Even the most ambitious project such as ASCI (Accelerated Strategic Computing Initiative) put the date to achieve 100 Tflops no sooner than 2003. So how we, just a handful of astrophysists with a limited budget, can outperform a national project with budget more than 1 billion dollars?
The answer is that we do not really outperform big projects like ASCI, since the goals are very different. The goal for ASCI machines is to provide a general-purpose high-performance computing platform, while our goal is much more limited. GRAPE-6 will be designed essentially for a single problem, namely the gravitational N-body problem. It will be much faster than ASCI (or any other) machine for N-body problem, but cannot even run a program for, say, grid-based CFD.
However, the limitation in the range of the application does not necessarily guarantee a better cost-performance. In fact, there have been a number of projects to develop special-purpose computers for various problems and only a handful of them can be regarded as success.
The basic reason for the success of GRAPE is that the problem itself allows us an extremely efficient use of available transistors. The number of transistors available on a chip increases by a factor of 100 in every decade, and the speed of the transistor increases by a factor of 10 in 10 years. Thus, if we can use all available transistors to do arithmetic operations, we can achieve the speedup by a factor of 1000 in 10 years.
In the case of general-purpose computers, the increase in the speed has been slower than this factor of 1000 in 10 years, since not all transistors are used for arithmetic operations. The fraction of the transistors used for arithmetic operations has been decreasing.
The reason for the decrease is that the speed of a processor is limited by the degree of parallelism and the data transfer bandwidth between processor and memory [McC95]. Even though we can integrate hundreds of arithmetic units in a chip, it is not easy to actually use all of them. In fact, it has become very difficult to provide the memory bandwidth sufficient for a single arithmetic unit.
The equation of motion for an N-body problem
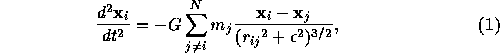
allows us to integrate a number of arithmetic units on a chip without problems either in the way to use them or in the memory bandwidth.
For parallelism, we can use three different approaches. The first is the pipeline specialized to the force calculation. With a pipelined structure, we can use 50 or more arithmetic units to calculate the force on a single particle. The second is to parallelize these pipelines to calculate the force on different particles, and the third is to use multiple pipelines to calculate the force on one particle. We can combine all these three approaches to reduce the requirement for the memory bandwidth by many orders of magnitude compared to what is required for a general-purpose computer.
The first approach, the pipelined processor specialized to one
application, has an additional advantage that the accuracy (and
therefore physical size) of each arithmetic unit can be optimized for
the operation it performs. Thus, if we do not need 64-bit accuracy for
an operation, we can reduce the accuracy of the arithmetic unit for
that operation, without sacrificing the overall accuracy. This has
been a very important factor for the early success of our machines
like GRAPE-1 [IMES90] and GRAPE-3 [OME 93].
93].
For GRAPE-4 with relatively high accuracy and massively parallel architecture, the latter two approaches played important roles. They will be even more important for GRAPE-6.