Previous ToC Next

 

7. 「とんでる力学」2005年 1 月分

7.1. プログラムと解説

赤木: というわけで、プログラムとかの解説ね。

学生S: あれ、 10-12 月分はどうしたんでしたっけ？

赤木: ちょっとさぼってるうちに時間がたってね。とりあえず、簡単 でまだ憶えてるところから手をつけるのがいいかと思ったの。 12 月はプログ ラムないし。 まず。図2のプログラムからね。あ、雑誌では図3だっけ？ 

   january-fig2.rb
  include Math
  unless File.exist?("january-fig2.ps")
    printer january-fig2.ps/vcps
    term
    square
    attackmax=20
    stallangle=15
    attackmin=-5
    viewport 0.1 1.1 0.1 1.1
    expand 2
    limit attackmin attackmax -0.1 1.1
    clcoef = 0.05
    xa=[]
    ya=[]
    (attackmin..attackmax).each{|i| xa.push(i)}
    xa.each{|x|
      if x <= stallangle
        y=x*clcoef
      else
        y=stallangle*clcoef*0.4
      end
      ya.push(y)
    }
    xdata xa
    ydata ya
    box BCNTSV  BCNTSV
    color 2
    conn
    ya=[]
    xa.each{|x|
      ya.push(0.01+x*x*0.0005)
    }
    ydata ya
    color 3
    conn
    color 4
    reloc attackmin 0.25
    draw  attackmax 0.25
    color 2
    reloc -10 0.85
    label C\\dL
    color 3
    reloc -10 0.75
    label C\\dD
    color 4
    reloc -10 0.65
    label c\\dm
  end

赤木: これは、 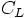と 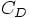のグラフを書くだけね。なんか それだけの割には長いけど。

学生S: とりあえず適当に書くだけならもっと簡単に書けます。でも、 いろいろ見かけとかを気にすると、細かい調整がいるから長くなるんです。別 に難しいことをしているわけではないです。

赤木: 一応簡単に説明してみて。

学生S: 最初の include は数学関数を使えるように mixin するだけで すね。これは何度もでてきてますが、 Math::sin とかする代わりに sin と書 けるようになります。 次の unless なんとかは、このプログラムでは1枚しか 書かないからあんまり関係ないんですが、図のファイルがあったら書かない、 というためのものです。 printer, square, viewport, expand, limit は全 部 Rongo のコマンドで、基本的な画面設定です。で、配列 xa, ya にいれた データからグラフを書くというのが Rongo では簡単なので、それを使ってま す。そのために、まず xa のほうに迎角の範囲で 1 づつかわる数字が入るよ うに、範囲方の each で値をいれて、次の xa.each のループで 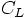の値 を計算して ya にいれます。

赤木: push ってなんだっけ？

学生S: これは、引数を配列の最後に追加するものです。 Ruby だと、 こんなふうで多くの場合に配列の添字を明示的に書く必要がないから、プログ ラムが短くなるし間違いも少ないと思います。

赤木: そうね。まあ、 C++ でも STL とかちゃんと使えば同じような ことができるはずだけど、ちょっと面倒だしね。

学生S: STL とか良く知らないです、、、

赤木: 作者も知らないと思うわ。 stallangle は失速角ね？

学生S: そうです。式が少しややこしいので、関数にしてもいいんですけど一度しか使わないものですし、、、

赤木: まあ、いいんじゃない？で、 xdata, ydata, box, color, connect でグラフを書くわけね。次は?

学生S: ya をクリアして、今度は 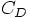のほうを書きます。

赤木: やってることは同じね。色が違うくらい？

学生S: です。そのあとの reloc, draw で 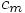の線を引いて、 あとはラベルを色々書いてるだけです。

赤木: まあ、こんなものよね。 Rongo のほうに、関数を与えてグラフを書かせるとか、そういうもうちょっと賢い機能が欲しいわね。

学生S: 作者にいって下さい。まあ、自分が必要と思えばそのうちに作るんではないですか？

赤木: そうね。図3のほうは？あ、雑誌では図4ね？

学生S: これです。 

   january-fig3.rb

  require 'vector.rb'
  include Math

  def cl(alpha)
    stallangle=15
    clcoef = 0.05
    x = alpha*180/PI
    if x <= stallangle
      y=x*clcoef
    else
      y=stallangle*clcoef*0.4
    end
    y
  end

  def cd(alpha)
    x = alpha*180/PI
    0.01+x*x*0.0005
  end

  def alphaexact(beta)
    alpha=-beta
    100.times{
      x = alpha+beta
      direction=atan2(cl(x),cd(x))
      alpha -= (direction-alpha)*0.003
      print( alpha, direction, "\n")

    }
    alpha
  end

  def thetaandv(alpha, beta, sstab)
    as = alpha+beta
    l = cl(alpha)+sstab*cl(as)
    d = cd(alpha)+sstab*cd(as)
    theta=atan2(d,l)
    ctotal=sqrt(l*l+d*d)
    v=sqrt(2/ctotal)
    [theta,v]
  end

  sstab=0.1

  unless File.exist?("january-fig3.ps")
    printer january-fig3.ps/vcps
    term
    square
    attackmax=20
    attackmin=1
    viewport 0.1 1.1 0.1 1.1
    expand 2
    limit attackmin attackmax -0.1 2
    xa=[]
    ya=[]
    ((attackmin*4)..(attackmax*4)).each{|i| xa.push(i*0.25)}
    box BCNTSV  BCNTSV

    xa.each{|x|
      beta=-x/180*PI
      ya.push(thetaandv(alphaexact(beta),beta,sstab)[1]/2)
    }
    xdata xa
    ydata ya
    color 2
    conn
    ya=[]
    xa.each{|x|
      beta=-x/180*PI
      ya.push(thetaandv(-beta,beta,0)[1]/2)
    }
    xdata xa
    ydata ya
    color 2
   # conn

    ya=[]
    xa.each{|x|
      beta=-x/180*PI
      ya.push(thetaandv(alphaexact(beta),beta,sstab)[0])
    }
    ydata ya
    color 3
    conn

    ya=[]
    xa.each{|x|
      beta=-x/180*PI
      ya.push(thetaandv(-beta,beta,0)[0])
    }
    ydata ya
    color 3
    conn

    ya=[]
    xa.each{|x|
      beta=-x/180*PI
      vdata=thetaandv(alphaexact(beta),beta,sstab)
      vsink = sin(vdata[0])*vdata[1]
      ya.push(vsink)
    }
    ydata ya
    color 4
    conn

    ya=[]
    xa.each{|x|
      beta=-x/180*PI
      vdata=thetaandv(-beta,beta,0)
      vsink = sin(vdata[0])*vdata[1]
      ya.push(vsink)
    }
    ydata ya
    color 4
    conn
  end

赤木: これはどこからみればいいのかしら？

学生S: 本体は unless File なんとかからです。これ以下は、基本的 には与えられた関数のグラフを書いているだけです。 

  xa.each{|x|
    beta=-x/180*PI
    ya.push(thetaandv(alphaexact(beta),beta,sstab)[1]/2)
  }

では ya に thetaandv が返す配列の2番目の要素を 2 で割ったものをいれて、 それを縦軸にしてグラフを書いているわけです。

赤木: thetaandv ってどういう関数なの？

学生S: 

 def thetaandv(alpha, beta, sstab)
   as = alpha+beta
   l = cl(alpha)+sstab*cl(as)
   d = cd(alpha)+sstab*cd(as)
   theta=atan2(d,l)
   ctotal=sqrt(l*l+d*d)
   v=sqrt(2/ctotal)
   [theta,v]
 end

ですね。 cl, cd がそれぞれ 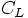と 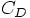を返す関数で、水平尾翼の分の補正をつけたあと 揚力/抗力 を計算して角度を求めています。で、速度は全空気力と重力がつり あうように決めるだけです。

赤木: alphaexact ってのは?

学生S: これは、あんまり意味はないですけど、水平尾翼の作るモー メントが、抗力も考えても 0 になるような迎角です。ほとんど alpha と同じ なので、ちょっと適当な方法で解いています。 

 def alphaexact(beta)
   alpha=-beta
   100.times{
     x = alpha+beta
     direction=atan2(cl(x),cd(x))
     alpha -= (direction-alpha)*0.003
     print( alpha, direction, "\n")

   }
   alpha
 end

です。

赤木: えーと、これあってる？

学生S: と思いますけど、、、つまり、 direction と alpha が等しく なるようにしてるわけで、 direction は水平尾翼への力の方向なわけです。 それは水平尾翼の CL, CD から与えられます。

赤木: うーん、なんかすぐにはわからないようなプログラムね。

学生S: 方程式を解くようなプログラムって、わかりやすいように書く のは難しいと思います。

赤木: まあね。達成したいものが素直に表現されるわけじゃないから。

学生S: 今回これくらいでいいことにしません？

赤木: そうね。プログラム動かしてみないと正しいかどうか良くわか らないしね。

Previous ToC Next