2. 「とんでる力学」6 月分
2.1. プログラムと解説
赤木: というわけで、先月に続いてプログラムとかの解説ね。
学生S: えーと、そうですね。まず図2 のグラフをどうやって書いたかです ね。とりあえずプログラム出してみましょうか。
# ballplot.rb (parity page version) require 'narray' include Math
$g=-9.8
$air_density = 1.3
class Ball
attr_accessor :mass, :radius, :rotations,
:cd, :alpha
def initialize(mass = 0, radius=0, rotations=0, cd=0,alpha=0)
@mass = mass
@radius=radius
@rotations=rotations
@cd=cd
@alpha=alpha
end
def area
PI*@radius*@radius
end
def lift(v)
area*v*@rotations*2*PI*radius*alpha*$air_density/@mass/2
end
def drag(v)
area*v*v*cd*$air_density*0.5/@mass
end
def dx(x)
d= NArray.float(4)
d[0]=x[2]
d[1]=x[3]
vabs = sqrt(x[2]*x[2]+x[3]*x[3])
lf= lift(vabs)/vabs
df= -drag(vabs)/vabs
d[2]= df*x[2]-lf*x[3]
d[3]= lf*x[2]+df*x[3]+$g
d
end
def rk2(x,dt)
d = dx(x)*0.5*dt
x += dx(x+d)*dt
x
end
end
def fig1
# term
printer june-fig1.ps/vcps
square
lw 2
viewport 0 1 0.6 1
limit 0 20 0 2
box
def plotsolution(x0,y0,vx0,vy0,b,dt)
x = NArray.float(4)
x[0..3]=[x0,y0,vx0,vy0]
prev=x[0..1]
time = 0
reloc x[0] x[1]
while (x[1] >= 0) and (time < 2000)
time += dt
x = b.rk2(x,dt)
if (x[0]-prev[0]>0.05) then
draw x[0] x[1]
prev=x[0..1]
end
end
end
b=Ball.new(0.15,0.035,30.0,0.4,1.2)
plotsolution 0,1,30,2 , b, 0.001
b=Ball.new(0.15,0.035,0.0,0.4,1.2)
plotsolution 0,1,30,2 , b, 0.001
b=Ball.new(0.15,0.035,-30.0,0.4,1.2)
plotsolution 0,1,30,2 , b, 0.001
lw 2
viewport 0 1 -1.5 -0.25
limit 0 100 0 50
box
vx=30*cos(PI/4)
vy=30*sin(PI/4)
b=Ball.new(0.15,0.035,30.0,0.4,1.2)
plotsolution 0,0,vx,vy , b, 0.004
b=Ball.new(0.15,0.035,30.0,0.0,0)
plotsolution 0,0,vx,vy , b, 0.004
b=Ball.new(0.15,0.035,0.0,0.4,1.2)
plotsolution 0,0,vx,vy , b, 0.004
end
def fig1a
# term
printer june-fig1a.ps/vcps
square
lw 2
viewport 0 1 0 1
limit 0 5 0 30
box
def plotsolution(x0,y0,vx0,vy0,b,dt)
x = NArray.float(4)
x[0..3]=[x0,y0,vx0,vy0]
prev=x[0..1]
time = 0
reloc time x[2]
while (x[1] >= 0) and (time < 2000)
time += dt
x = b.rk2(x,dt)
if (x[0]-prev[0]>0.05) then
draw time x[2]
prev=x[0..1]
end
end
end
vx=30*cos(PI/4)
vy=30*sin(PI/4)
b=Ball.new(0.15,0.035,30.0,0.4,1.2)
plotsolution 0,0,vx,vy , b, 0.004
b=Ball.new(0.15,0.035,30.0,0.0,0)
plotsolution 0,0,vx,vy , b, 0.004
b=Ball.new(0.15,0.035,0.0,0.4,1.2)
plotsolution 0,0,vx,vy , b, 0.004
end
def calculatedistance(vabs0,angle,b,dt)
x = NArray.float(4)
theta=angle*PI/180
x[0..3]=[0,0,vabs0*cos(theta),vabs0*sin(theta)]
prev=x
time=0
while x[1] >= 0
prev=x
x = b.rk2(x,dt)
time+= dt
end
frac = -prev[1]/(x[1]-prev[1])
prev[0]+frac*(x[0]-prev[0])
end
def plotdist(b)
for s in 10..30
angle=s*2.0
dist = calculatedistance(30, angle, b, 0.001)
if s == 10
reloc angle dist
else
draw angle dist
end
end
end
def fig2
# term
printer june-fig2.ps/vcps
square
lw 2
viewport 0 1 0 1
limit 20 60 50 90
box
b=Ball.new(0.15,0.035,30.0,0.4,1.2)
plotdist b
b=Ball.new(0.15,0.035,60.0,0.4,1.2)
plotdist b
b=Ball.new(0.15,0.035,0.0,0.4,1.2)
plotdist b
end fig1 pgend psfix fig1a pgend psfix fig2 pgend psfix
赤木: 随分長いわね。 200 行もあるわよ。
学生S: やることが複雑なので、、、図2を書くのは実際には fig1 と いう名前の関数、
def fig1
# term
printer june-fig1.ps/vcps
square
lw 2
viewport 0 1 0.6 1
limit 0 20 0 2
box
def plotsolution(x0,y0,vx0,vy0,b,dt)
x = NArray.float(4)
x[0..3]=[x0,y0,vx0,vy0]
prev=x[0..1]
time = 0
reloc x[0] x[1]
while (x[1] >= 0) and (time < 2000)
time += dt
x = b.rk2(x,dt)
if (x[0]-prev[0]>0.05) then
draw x[0] x[1]
prev=x[0..1]
end
end
end
b=Ball.new(0.15,0.035,30.0,0.4,1.2)
plotsolution 0,1,30,2 , b, 0.001
b=Ball.new(0.15,0.035,0.0,0.4,1.2)
plotsolution 0,1,30,2 , b, 0.001
b=Ball.new(0.15,0.035,-30.0,0.4,1.2)
plotsolution 0,1,30,2 , b, 0.001
lw 2 viewport 0 1 -1.5 -0.25 limit 0 100 0 50 box vx=30*cos(PI/4) vy=30*sin(PI/4) b=Ball.new(0.15,0.035,30.0,0.4,1.2) plotsolution 0,0,vx,vy , b, 0.004 b=Ball.new(0.15,0.035,30.0,0.0,0) plotsolution 0,0,vx,vy , b, 0.004 b=Ball.new(0.15,0.035,0.0,0.4,1.2) plotsolution 0,0,vx,vy , b, 0.004 end
ですから、ここからみていきましょうか?
赤木: その前に、class って何かというのをちょっと説明してよ。
学生S: うーん、ちゃんとした説明は Ruby の適当な本をみて欲しいん ですが、
class Foo ここに何か書く
end
でクラスを定義できます。クラスとはそもそもなにかというのが問題ですが、 えーと、基本的には C の構造体みたいな、自分で定義するデータ型です。 初期化関数
def initialize(mass = 0, radius=0, rotations=0, cd=0,alpha=0)
@mass = mass
@radius=radius
@rotations=rotations
@cd=cd
@alpha=alpha
end
を定義しておくと、 x = Ball.new(0,0,0,0,0) とか<tt> x = Ball.new</a> とか書くことで Ball 型の変数ができる、というわけです。
単なる構造体と違うのは、そのメンバーとして変数だけでなく関数も定義でき ることです。C++ のクラスではそういう関数をメンバー関数といいますが、 Ruby ではメソッドといいます。上の initialize もメソッドですが、 これは特別で Ball.new が勝手に呼び出すものです。それ以外は、 x が Ball 型なら、というか、それを Ball クラスのインスタ ンスなら、ということが多いですが、そうなら、 x.fig1 みたいな 形で呼べるわけです。
赤木: 単に x を引数に取る fig1(x) という関数となに か違うのかしら?
学生S: 計算機の動作は変わらないです。プログラムは、メソッドの中 ではクラスで定義された変数が x.mass の代わりに @mass と書けるとか、それくらいの違うしかないといえなくもないです。でも、そう いうことでいくらか書きやすかったり読みやすかったりすると思います。
赤木: まあ、そうね。後は継承とかいろんな便利なことがあるわけだ けど、今回使ってないわね。
学生S: ええ。とりあえず深く考えないで書いてますし。
赤木: で、 fig1 よね。最初のほうは例によって rongo の コマンドね。 term がコメントアウトしてあって、 printer が生きてる のは最終的には PS ファイルを作るからね。切換えるのはどうするの?
学生S: どうって、プログラムを書き変えます。どうせプログラムはエ ディタで開いていて、細かい修正をして最終的なグラフを出すので、あんまり 別ファイルからパラメタ読むとかしても面倒なだけですし。
赤木: そうでしょうね。コンパイルして実行とかいうとちょっと面倒 だったり時間がかかったりするけど、 Ruby はインタプリタだものね。次の plotsolution は?
学生S: これは実際に常微分方程式を解いて結果をプロットします。 パラメタというか引数は、初期条件、 Ball クラスの変数、これは質量とか半 径とか回転速度とかをもってるわけですが、である b と時間刻み dt で す。 プログラムは見ての通りで、 while ループの中で時間を進めて、 +rk2+ を呼んで積分して、 x 座標の値、つまり x[0] が前 にプロットした時からある程度、この場合には 0.05 変わっていたら線を引く だけですね。 rk2 は先月と同じです。
赤木: 方程式はどこで定義してるの?
学生S: これはメソッド dx ですね。
def dx(x)
d= NArray.float(4)
d[0]=x[2]
d[1]=x[3]
vabs = sqrt(x[2]*x[2]+x[3]*x[3])
lf= lift(vabs)/vabs
df= -drag(vabs)/vabs
d[2]= df*x[2]-lf*x[3]
d[3]= lf*x[2]+df*x[3]+$g
d
end
lift と drag という関数で揚力、抗力を計算して、揚力は進行方向に垂 直、抗力は並行で逆向きに働かせています。 lift, drag はそれぞ れ 1 行で
def lift(v)
area*v*@rotations*2*PI*radius*alpha*$air_density/@mass/2
end
def drag(v)
area*v*v*cd*$air_density*0.5/@mass
end
で、本文の式に従って値を計算するだけです。 area は  で面積を計算する関数
で面積を計算する関数
def area
PI*@radius*@radius
end
です。
赤木: ふむ、まあいいでしょう。後はボールのパラメタとか初期条件 を変えて plotsolution を何度も呼ぶだけね。次のグラフは?
学生S: 関数は fig1a です。
def fig1a
# term
printer june-fig1a.ps/vcps
square
lw 2
viewport 0 1 0 1
limit 0 5 0 30
box
def plotsolution(x0,y0,vx0,vy0,b,dt)
x = NArray.float(4)
x[0..3]=[x0,y0,vx0,vy0]
prev=x[0..1]
time = 0
reloc time x[2]
while (x[1] >= 0) and (time < 2000)
time += dt
x = b.rk2(x,dt)
if (x[0]-prev[0]>0.05) then
draw time x[2]
prev=x[0..1]
end
end
end
vx=30*cos(PI/4)
vy=30*sin(PI/4)
b=Ball.new(0.15,0.035,30.0,0.4,1.2)
plotsolution 0,0,vx,vy , b, 0.004
b=Ball.new(0.15,0.035,30.0,0.0,0)
plotsolution 0,0,vx,vy , b, 0.004
b=Ball.new(0.15,0.035,0.0,0.4,1.2)
plotsolution 0,0,vx,vy , b, 0.004
end
赤木: 関数の名前と図の名前が違うと後で混乱しない?
学生S: するかもしれないですけど、とりあえず出版されてしまってこ の原稿も書いてしまえば、あんまり変更もしないし、それにほら、ここで違う ということを記録に残しておけば、混乱してもなんとかなるんじゃないですか?
赤木: 3ヶ月先の自分は他人ということもあるからあんまり良くないと 思うけど、まあいいでしょう。実際あなたが2ヶ月前に書いたプログラムを今解説してもらってるしね。
学生S: 見てると結構思い出すものです。
赤木: これ、やってることは fig1 とほとんど変わらないみ たいだけど、 プロットしてるものは違うわよね、、、あ、 plotsolution を再定義してるのね。 インタプリタだからこういうこともできるわけか。
学生S: そういうことですね。
赤木: でも、ほとんど同じものを、コピーペーストでできるといって も2つ書くのは美しくないし、後で変更した時におかしくなるとかしない?
学生S: うーん、むしろ図2と図3で全然別の関数を使ってるというほう が、図2を変更したら 3 も変わってしまったなんてことがなくて安全な気もし ます。
赤木: それは、確かにそういう面もあるのよね。なかなか難しいとこ ろね。
学生S: まあ、これ書いた時には plotsolution を共通にする簡単な 方法を思い付かなかったせいもあるんですけど。
赤木: これ書いた時には、っていうと、今ならもうちょっとましに書 けるの?
学生S: と思います。でも、この話は次回、っていうか、7月号の分はプログラムないですから、8月号の分にしませんか?
赤木: そね、時間もないし。
学生S: そういうわけで、 plotsolution は軌跡の代わりに時刻と
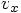 を書くというだけですね。それ以外は、軸の範囲が違うく らいです。
を書くというだけですね。それ以外は、軸の範囲が違うく らいです。
赤木: 図4は?
学生S: これはだいぶ違いますね。
def fig2
# term
printer june-fig2.ps/vcps
square
lw 2
viewport 0 1 0 1
limit 20 60 50 90
box
b=Ball.new(0.15,0.035,30.0,0.4,1.2)
plotdist b
b=Ball.new(0.15,0.035,60.0,0.4,1.2)
plotdist b
b=Ball.new(0.15,0.035,0.0,0.4,1.2)
plotdist b
end
ですが、plotfunction の代わりに plotdist という関数を作ってます。
赤木: これがメソッドでなくて普通の関数なのはなんか意味があるの?
学生S: すみません、ないです。メソッドのほうが良かったかも。
赤木: こういうちょっとしたことからプログラムってわかりにくくな るから、、、まあ、いいでしょう。 plotdist の中身は?
学生S: これですね。
def plotdist(b)
for s in 10..30
angle=s*2.0
dist = calculatedistance(30, angle, b, 0.001)
if s == 10
reloc angle dist
else
draw angle dist
end
end
end
角度を 20 度から 60 度まで2度づつ変化させて、 calculatedistance で距 離を計算してグラフを書く、というだけです。 calculatedistance のほうはこんなので:
def calculatedistance(vabs0,angle,b,dt)
x = NArray.float(4)
theta=angle*PI/180
x[0..3]=[0,0,vabs0*cos(theta),vabs0*sin(theta)]
prev=x
time=0
while x[1] >= 0
prev=x
x = b.rk2(x,dt)
time+= dt
end
frac = -prev[1]/(x[1]-prev[1])
prev[0]+frac*(x[0]-prev[0])
end
初期条件から y が負になるまで計算して、負になったら負になる直前の値 と線型補間して y が 0 になる x の値を計算して、それを返すというふうにしています。
赤木: なるほど、まあ、いいんじゃない?来月はプログラムないから、 一回休みね。