


Next: 5 Summary and Discussion
Up: A 1.349 Tflops
Previous: 3 The GRAPE-6 system
We have simulated the evolution of a galactic nucleus containing
triple massive black holes. As we stated in the introduction,
currently available numerical simulations suggest that when two
galaxies merge, their central black holes will be left as a binary
system. Thus, when the remnant of a galaxy merger again merges with a
third galaxy, the final merged object is likely to host three massive
black holes.
The evolution of a triple black hole system is entirely different from
that of a binary system, since it is very unlikely that three black
holes form a dynamically stable system. There are basically two
possibilities for the final outcome. One is that one or more black
holes will be ejected from the galaxy through three-body interaction
of black holes (gravitational slingshot,
[SVA74]). The other possibility is that
during the three-body interaction two black holes come close enough
that they merge through gravitational wave radiation
[HR92,ME94]. Thus, even after black holes
have kicked out all nearby stars, they can still evolve in a complex
way. On the other hand, a bound pair of two black holes is always
dynamically stable. Thus, once a binary has kicked out all nearby
stars, the evolution would be completely halted.
As we have described in the introduction, several numerical studies on
the evolution of the massive black hole binary have been published,
but to our knowledge there is no self-consistent N-body simulation
of the black hole triples embedded in the galactic core, though the
potential importance was first pointed out a number of years ago
[SVA74] and studied in a number of papers
both theoretically and numerically as a pure three-body problem in the
fixed background potential (see [Val99] for a recent example).
The primary reason for this non-existence of the direct numerical work
is the same difficulty of simulation as we described in the
introduction for the case of the black hole binary. Though the
evolution of the black holes might be different, the numerical
difficulties are all the same. Since the difficulties are the same,
the same solution, the combination of GRAPE hardware and individual
timestep algorithm, works rather well for this problem.
In our simulation, the galaxy is modeled with 786,432 equal-mass
stars. The black holes are modeled as three point-mass particles
with a mass of 1% of the total mass of the system. The
relativistic effects were neglected in our simulation. The
gravitational force from black holes, both on field stars and on black
holes, are calculated on the host computer to ensure the best possible
accuracy. The force from field particles is calculated on GRAPE-6.
We performed a simulation for 7.875 dynamical time units, for which the
number of individual steps was 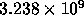 . The whole
simulation, including on-the-fly analysis of the orbital elements
of black holes and file operations, took 29.88 hours. The total number
of floating point operations is
. The whole
simulation, including on-the-fly analysis of the orbital elements
of black holes and file operations, took 29.88 hours. The total number
of floating point operations is 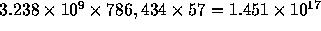 , since one particle-particle
interaction amounts to 57 floating point operations. The resulting
average computing speed is 1.349 Tflops.
, since one particle-particle
interaction amounts to 57 floating point operations. The resulting
average computing speed is 1.349 Tflops.
The calculation reported here is the first large simulation of black
hole triples in the core of the galaxy, and as such, the result turned
out to be rather surprising. Figure 12 shows the
evolution of the orbital elements for the most strongly bounded pair
of binaries. The criterion of the selection of the pair is that the
binding energy is the maximum. The binding energy of two black holes
i and j
is defined as
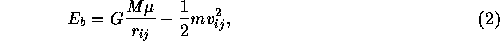
where M is the total mass 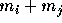 ,
, 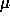 is the reduced mass
defined as
is the reduced mass
defined as 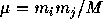 , and
, and 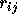 and
and 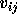 are the
relative distance and relative velocity of the pair.
We regard this most strongly bounded pair as binary and plotted the
time evolution of its semi-major axis and eccentricity. The evolution
of the semi-major axis is not much different from those in the
simulations of black hole binaries. However, the behavior of the
eccentricity is quite different. In simulations of black hole
binaries, it was found that the eccentricity remains almost constant
during the evolution, and typically eccentricity is not very
large. Thus, black holes do not come close to each other, and the
effect of gravitational radiation remains small. In figure
12, however, we can see that the eccentricity e
comes very close to 1 rather frequently (note that we plotted
1-e). The effect of the gravitational radiation is
proportional to
are the
relative distance and relative velocity of the pair.
We regard this most strongly bounded pair as binary and plotted the
time evolution of its semi-major axis and eccentricity. The evolution
of the semi-major axis is not much different from those in the
simulations of black hole binaries. However, the behavior of the
eccentricity is quite different. In simulations of black hole
binaries, it was found that the eccentricity remains almost constant
during the evolution, and typically eccentricity is not very
large. Thus, black holes do not come close to each other, and the
effect of gravitational radiation remains small. In figure
12, however, we can see that the eccentricity e
comes very close to 1 rather frequently (note that we plotted
1-e). The effect of the gravitational radiation is
proportional to 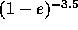 . Thus, if
. Thus, if 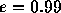 , the effect of
gravitational radiation is
, the effect of
gravitational radiation is 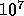 times stronger than in the case of a
circular binary. Thus, it is quite likely that this bound pair emits
strong gravitational radiation resulting in the merging of two black
holes.
times stronger than in the case of a
circular binary. Thus, it is quite likely that this bound pair emits
strong gravitational radiation resulting in the merging of two black
holes.
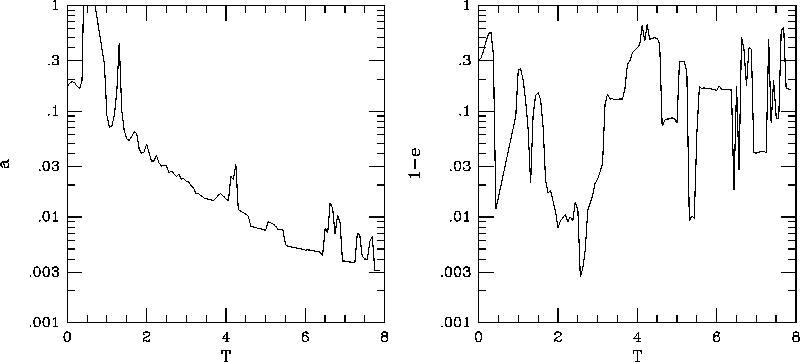
Figure 12: The time evolution of the semi-major axis (left panel) and
eccentricity (right panel) of the most strongly bounded pair of black
holes.
Since the variation of the eccentricity is highly stochastic, we need
more simulations from different initial conditions, and it is
desirable to incorporate the effect of the gravitational radiation
directly into the simulation to see if it actually works. However, our
present result clearly demonstrates the importance of the triple
interaction.
As a short benchmark run, we tried the same simulation with 1,400,000
stars for 0.25 time units. For this run, the total number of timesteps
is 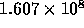 , and calculation took 2.17 hours. The average
calculation speed was 1.64 Tflops.
, and calculation took 2.17 hours. The average
calculation speed was 1.64 Tflops.



Next: 5 Summary and Discussion
Up: A 1.349 Tflops
Previous: 3 The GRAPE-6 system
Jun Makino
Sun Jul 30 15:33:07 JST 2000
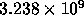 . The whole
simulation, including on-the-fly analysis of the orbital elements
of black holes and file operations, took 29.88 hours. The total number
of floating point operations is
. The whole
simulation, including on-the-fly analysis of the orbital elements
of black holes and file operations, took 29.88 hours. The total number
of floating point operations is 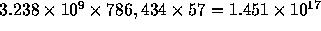 , since one particle-particle
interaction amounts to 57 floating point operations. The resulting
average computing speed is 1.349 Tflops.
, since one particle-particle
interaction amounts to 57 floating point operations. The resulting
average computing speed is 1.349 Tflops.
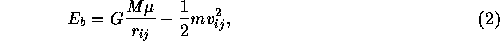
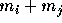 ,
, 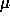 is the reduced mass
defined as
is the reduced mass
defined as 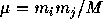 , and
, and 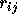 and
and 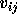 are the
relative distance and relative velocity of the pair.
We regard this most strongly bounded pair as binary and plotted the
time evolution of its semi-major axis and eccentricity. The evolution
of the semi-major axis is not much different from those in the
simulations of black hole binaries. However, the behavior of the
eccentricity is quite different. In simulations of black hole
binaries, it was found that the eccentricity remains almost constant
during the evolution, and typically eccentricity is not very
large. Thus, black holes do not come close to each other, and the
effect of gravitational radiation remains small. In figure
are the
relative distance and relative velocity of the pair.
We regard this most strongly bounded pair as binary and plotted the
time evolution of its semi-major axis and eccentricity. The evolution
of the semi-major axis is not much different from those in the
simulations of black hole binaries. However, the behavior of the
eccentricity is quite different. In simulations of black hole
binaries, it was found that the eccentricity remains almost constant
during the evolution, and typically eccentricity is not very
large. Thus, black holes do not come close to each other, and the
effect of gravitational radiation remains small. In figure
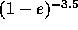 . Thus, if
. Thus, if 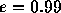 , the effect of
gravitational radiation is
, the effect of
gravitational radiation is 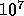 times stronger than in the case of a
circular binary. Thus, it is quite likely that this bound pair emits
strong gravitational radiation resulting in the merging of two black
holes.
times stronger than in the case of a
circular binary. Thus, it is quite likely that this bound pair emits
strong gravitational radiation resulting in the merging of two black
holes.

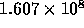 , and calculation took 2.17 hours. The average
calculation speed was 1.64 Tflops.
, and calculation took 2.17 hours. The average
calculation speed was 1.64 Tflops.