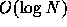 , since the cost is proportional to the number
of levels of the tree.
, since the cost is proportional to the number
of levels of the tree.
The basic idea of the tree algorithm is to replace the gravitational forces from distant particles with the force from their center of mass, or with multipole expansion if high accuracy is desired. Particles are organized into an octree structure, with the root node covering the entire system and leafs corresponding to each particles.
The force on a particle from a node is defined (and calculated)
recursively. If the node and particle are well separated (in terms
of the error of the multipole expansion), the force from the node to
the particle is calculated by evaluating the multipole expansion of
the node at the location of the particle. If they are not well
separated, the force is evaluated as the sum of the forces from
children of the node. The calculation cost of the force on one
particle is 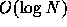 , since the cost is proportional to the number
of levels of the tree.
, since the cost is proportional to the number
of levels of the tree.
In order to use the multipole expansions of the nodes, they must be
precomputed. The expansion coefficients for a node can be recursively
calculated from those of children nodes. The calculation cost of this
part is 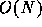 .
.
For details of implementation, see [13]. Salmon et al. [15] describes the implementation of the tree algorithm on distributed-memory parallel computers.
In the tree algorithm, the particles which generate the gravitational potential and the particles which feel the potential are not symmetric. The particles which generate potential are treated as clumps whenever possible. However, calculations of the forces on two particles are totally independent, even though the two particles are in small distance.
The basic idea of FMM (Fast Multipole Method, [6,7]) is to locally expand the potential field and use that expansion to obtain the forces on multiple particles. Figure 1 shows the relation between the tree algorithm and FMM.

Figure 1: Approximations in tree (top) and FMM(bottom)
Since neighboring particles share the same expansion, the scaling of
the calculation cost changes from 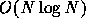 of the tree algorithm
to
of the tree algorithm
to 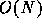 . However, for similar accuracy, the actual calculation cost
of FMM is significantly higher than that of tree algorithm, even for
very large number of particles.
[4]
. However, for similar accuracy, the actual calculation cost
of FMM is significantly higher than that of tree algorithm, even for
very large number of particles.
[4]
The fundamental reason for the relatively high cost of FMM is that the
scaling with the order of the expansion is different. In three
dimensions, the calculation cost of the tree algorithm is 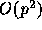 ,
where p is the order of the multipole expansion. The number of
independent terms of the spherical harmonics of order p is
,
where p is the order of the multipole expansion. The number of
independent terms of the spherical harmonics of order p is
 . Since the evaluation of terms can be done using recurrent
relation, the calculation cost is proportional to the number of terms.
On the other hand, the calculation cost of FMM is
. Since the evaluation of terms can be done using recurrent
relation, the calculation cost is proportional to the number of terms.
On the other hand, the calculation cost of FMM is 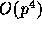 , since the
translation of the multipole expansion to the local expansion requires
the calculation cost proportional to the square of the number of
terms.
, since the
translation of the multipole expansion to the local expansion requires
the calculation cost proportional to the square of the number of
terms.
Of course, it is possible to reduce this 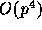 scaling to
scaling to
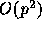 , by increasing the number of particles at the lowest
cell. Also, it is possible to apply FFT to the translation
[5] to reduce
, by increasing the number of particles at the lowest
cell. Also, it is possible to apply FFT to the translation
[5] to reduce 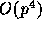 scaling to
scaling to 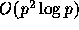 . When these two are combined, the resulting scaling is
. When these two are combined, the resulting scaling is
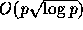 . However, it should be noted that FFT is
advantageous only for very large values of p. Even for pretty large
values of p, the gain by FFT does not exceed a factor of two.
In addition, FFT works fine for non-adaptive variant of FMM, but might
not work so well for an adaptive version.
. However, it should be noted that FFT is
advantageous only for very large values of p. Even for pretty large
values of p, the gain by FFT does not exceed a factor of two.
In addition, FFT works fine for non-adaptive variant of FMM, but might
not work so well for an adaptive version.
At present, FMM does not offer clear advantage in performance compared to the tree algorithms. One of the reason is that the mathematics used in FMM is much more complex and therefore it is more difficult to implement FMM than to implement the tree algorithm. As a result, relatively small number of implementations exist for FMM. These implementations are not widely used and not very highly optimized. Since FMM is a complex algorithm, there are many small places which can easily lead to rather large inefficiency. The tree algorithm is much simpler and therefore easier to achieve high efficiency.
Anderson [1] proposed an alternative formulation of FMM which is based on Poisson's formula. In two dimensions, the gravitational potential outside a disk of radius a containing particles is expressed as
where G is the gravitational constant, M is the total mass of the
particles in the disk, 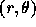 is the position in polar
coordinate. This formula gives the solution of the boundary value
problem of the Laplace equation.
is the position in polar
coordinate. This formula gives the solution of the boundary value
problem of the Laplace equation.
In order to use formula (1) as an replacement of the
multipole expansion, the integral must be replaced by some numerical
quadrature. The ``best'' method for the numerical integration over a
circle is to distribute the points in equal spacing and sum the values
on these points with equal weights. When we use 2p+1 points to
sample potential, the integration should give exact values for p-th
order terms in multipole expansion. Note that the p-th term in the
multipole expansion corresponds to p-th term in the Fourier
expansion of the potential on the circle 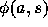 .
.
Anderson found that the naive use of the numerical quadrature in combination with formula (1) gives unacceptable result. The reason is that finite number of sampling points introduces fictitious high-frequency terms in Fourier components. In order to suppress high-frequency terms, we should truncate the multipole expansion at order p. In other words, formula (1) should be replaced by
With this modification, Anderson successfully used Poisson's formula to implement FMM. The local expansion can also given in a similar form.
In three dimensions, the outer and inner expansions are given by
and
In actual implementation, the infinite sum must also be truncated at the order of the integration scheme used.
In two dimensions, the trapezoidal rule is optimum and is directly
related to the Fourier expansion. However, in three dimensions, the
way to assign points on a sphere is not unique. Anderson followed the
formula given in [11], which claims to have constructed
5th, 7th, 9th, 11th and 14th order integration formulae with 12, 24,
32, 50 and 72 points. Recently, Hardin and Sloane
[9] suggested a complete set of the achievable
orders for integration schemes with up to 100 points. They called an
integration schemes which achieved order t as t-designs. Table
2.3 gives the summary of their result. Note that a
D-th order scheme (D-design) can express spherical harmonics of
the order only up to 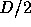 [1].
[1].
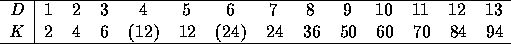
Table 1: number of points K and achievable order D
For orders 2, 3 and 5, the corresponding distributions of points are the vertices of tetrahedron(K=4), octahedron(K=6) and icosahedron (K=12).
Blackston and Suel [4] implemented both the classical FMM and Anderson's method, and found that for similar accuracy the latter is faster typically by a factor of few.
The most significant practical advantage of Anderson's method is the ease of the implementation. The classical FMM in three dimensions requires rather complex formulas to be implemented for the shifting the center of the the multipole expansion (``M2M'' part), translation of the multipole expansion to local expansion (``M2L'' part) and shifting the center of the local expansion (``L2L'' part). In Anderson's method, all shiftings and translations are realized by evaluating the potential on the sample points on the sphere. Thus, all mathematics are confined into formulae (4) and (3).